Különleges napóra szerkesztések

BEVEZETÉSKÉNT

A
napórát tekinthetjük egy egyszerű felépítésű, analóg
számítógépnek, amely a bemeneti adatokat a napóra jellemzőinek
segítségével kimeneti adatokká alakítja. Bemenő adatok a Nap
napi csillagászati koordinátái: a deklináció és az óraszög,
illetve az ezeknek megfelelő és helyben érzékelhető irány- és
a magassági szögek. Kimeneti adatok: az óravonalakkal jelzett
irányszögek és a hónapok mentén leolvasható távolságok. A
napóra jellemzői: a hely földrajzi szélessége, valamint az
árnyékvető illetve a skála felület alakját és helyzetét
megadó szögek és távolságok.

A
napórák viszonylag egyszerű, hagyományos változatai a fali és
asztali napórák. Ezek óravonalai egymáshoz mérten a napóra
jellemzőitől függően, különböző szögekben állnak. Mégis
igény lehet például, hogy előírjuk egyes skálavonalak helyét –
alakját. Effajta lehetőségek megvalósítására alkalmasak az
egyébként is látványos megjelenésű kétszálas napórák.

Ezek
olyan napórák, amelyeknek az árnyékvetőjét nem egy pálca (rúd,
gnomon), hanem alapesetben a skálával párhuzamos síkokban lévő,
egymáshoz képest kitérő helyzetű, két árnyékvető szál
(drót, vékony pálca, kötél, lánc) alkotja. A szálakat és az
árnyékfelfogó síkot, továbbá a számított skálát a
méretezésnek megfelelő helyen és formában kell egymáshoz
illeszteni.

A
KÉTSZÁLAS NAPÓRA

A
kétszélas órák működésének alapja roppant szellemes és
egyszerű ötlet: nem kell semmilyen árnyékvető rúd, elég csak a
rúd végpontját megjelölni két, egymást keresztező szál
egybeeső pontjával. A skálával párhuzamos, felette azonos
távolságra lévő szálakkal bíró napóráknak a működési elve
és a skála számítási képletei pontosan azonosak a szokványos
elrendezésű asztali vagy fali órákéval. A szálak közös
pontjának árnyéka naponta a Nap deklinációja és a földrajzi
hely megszabta körkúp, valamint az ezt metsző skálasík által
meghatározott metszésvonal szerinti hiperbola mentén fog mozogni.
Ezen a görbén ott lesznek a napi időpontok osztásvonalai, mint
ahol a szokványos, pólusra irányuló árnyékvető vagy a
megfelelő gnomonhoz és csúcspontjához szerkesztett skálapontok
vannak.

A
Nap helyzetének változását mindkét szál árnyéka úgy követi,
hogy az árnyékok párhuzamosak maradnak az árnyékvető szálukkal
és így korábbi helyzetükkel is. Ha a szálak magassága eltérő,
a mozgások jellege nem változik, de a szálárnyékok mozgási
sebessége már egymástól eltérő mértékű lesz. A skálához
közelebbi szál árnyéka időegység alatt kisebb mértékben
mozdul el, a távolabbi nagyobb mértékben, Így a gnomon
végpontjának árnyékához képest a két szál árnyékának
metszéspontjai már más helyekre kerülnek, azaz a skála a gnomon
skálájához viszonyítva “torzul”. Ha a szálak irányai és
magasságuk az árnyékfogó síknak megfelelő követelményeket is
kielégítik, a napóra óravonalainak osztásköze egyenletesen
15-15 fok lesz (ugyanúgy, mint az egyenlítői síkkal párhuzamos
napóraváltozaté). Az ilyen vízszintes elrendezés az egyenszögű
kétszálas
asztali napóra.

AZ ASZTALI
NAPÓRÁK

A
legegyszerűbb ilyesfajta szerkezet az olyan kétszálas asztali
napóra, amelynél az egyik szál a helyi délkör síkjában van,
azaz Észak-Dél irányú és a másik szál erre merőleges, azaz
Kelet-Nyugat irányú. Innen adódik, hogy az egyik szálat délköri
szálnak, a másikat
keresztszálnak
célszerű nevezni. Egyébként ennek az elnevezésnek csak az
asztali napóránál van közvetlen értelme, mert a déltől
elfordult, függőleges falak napóráinál már nem szükségszerűen
van (de lehet!) függőleges délköri és vízszintes keresztszál.

A
nem egy síkban lévő két szállal bíró asztali napórák
skálájának meghatározásához vizsgáljuk a vízszintes síkon,
függőlegesen álló G
árnyékvető rúd csúcspontja (“gnomon-csúcs”)
által vetett P[x(t),y(t)]
árnyékpont koordinátái az 1.
ábra szerint.

Függőleges
gnomon árnyéka vízszintes síkon.

Legyen
a függőleges rúd a φ
földrajzi szélességű helyen egy olyan derékszögű, egyenközű
koordinátarendszer 0
középpontjában, amelyiknek x
tengelye Kelet felé, az y
tengelye Észak felé mutat. A vizsgálat t
(helyi) időpillanatában legyen a Nap időszöge τ,
deklinációja δ,
továbbá a helyi koordináták szerinti irányszöge A(δ,τ),
és magassági szöge m(δ,τ).
Mint ismeretes,

sin(m)
= sin(φ)×sin(δ)+cos(φ)×cos(δ)×cos(τ)

vagy

Miként
az 1. ábra mutatja, a G
rúd 1
jelű végpontjának árnyéka a vízszintes alapsíkon a 2
jelű pontban van. Legyen a μ
(az 140
lapszög) a délköri
emelkedési szög,
az η
(az 130
lapszög) a keresztirányú
emelkedési szög,
az M
(az 124
élszög) a keresztirányú
hajlásszög
és az N
(az 123
élszög) a délköri
hajlásszög.

Az
ábra nyomán a gúla egyes derékszögű háromszögeire felírt
trigonometriai alapösszefüggésekből kaphatunk olyan egyenleteket,
amelyekből leveethetők a gnomon köré rajzolt gúla szög- és
oldaladatai közti kapcsolatok, és ezekből a keresett x(t),
y(t)
vagy inkább az x(τ), y(τ)
koordinátáknak a Nap A(δ,τ),
m(δ,τ)
pillanatnyi adataitól függő értékei. A levezetések részletezése
nélkül a legfontosabb összefüggések:

y
=
G/tan(μ) x
= y×tan(A)

sin(m)
= sin(μ)×sin(M)
= sin(η)×sin(N)

tan(η)
= tan(m)/sin(A) tan(μ)
= tan(m)/cos(A)

tan(N)
= tan(μ)/sin(η) tan(M)
= tan(η)/sin(μ)

tan(M)/tan(N)
= tan(η)/tan(μ) tan(M)×tan(N)
= 1/cos(η)×cos(μ)

cos(N)
= cos(m)×cos(A) cos(M)
= cos(m)×sin(A)

Ezekben
a kifejezésekben az A(δ,τ),
m(δ,τ)
Nap-jellemzők közvetítésével, többszörösen is szerepel a t
→τ
idő,
így ezek az összefüggések csak nehézkesen használhatók. E
képleteket némileg átalakítva és egyszerűbb írásmódú
jelölésekkel ekképp fogjuk használni:

sin(m)
= sin(φ)×sin(δ)+cos(φ)×cos(δ)×cos(τ)
=

=
cos(φ)×cos(δ)×[cos(τ)+C₂]
=

=
cos(φ)×cos(δ)×q

C₁
= tan(δ)/tan(φ)
C₂
= tan(δ)×tan(φ)

p
= [cos(τ)-C₁] q
= [cos(τ)+C₂]

Ezeket
behelyettesítve az árnyékpont koordinátáit leíró
kifejezésekbe, egyszerüsítések után a gnomoncsúcs
árnyékpontjának időfüggvényei a vízszintes síkon, egyszerűbb
alakban:

A
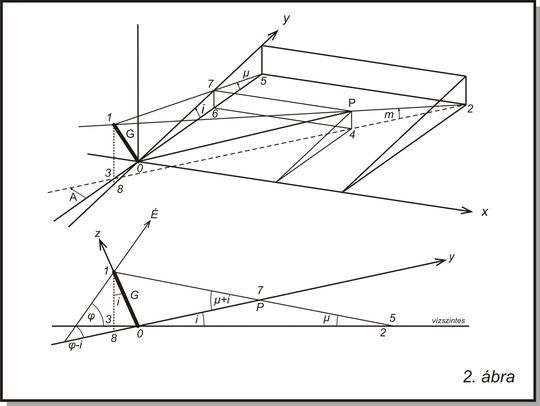
kiindulási feltételeket még általánosítsuk egy kissé.
Tekintsük a 2. ábra szerint egy olyan ferde síkot, amely i
szöggel emelkedik Észak felé. A G
árnyékvető rúd most is álljon merőlegesen az árnyékfelfogó
síkra, annak 0
pontjában. Legyen a derékszögű helyi koordinátarendszer y
tengelye a lejtősik és az É-D irányú délköri sík
metszésvonala, az x
tengelye
a lejtőnek az a vonala, amelyben a vízszintes alapsík és a lejtő
metszik egymást, a többi jellemző azonos az előző ábráéval.

Függőleges
gnomon árnyéka lejtős síkon.

A
G
rúd 1
jelű végpontjának árnyéka most is a vízszintes alapsíkon a 2
jelű pontban lenne, ha átlátszó lenne az árnyékfelfogó sík.
Mivel ez nem átlátszó, a rúd csúcspontjának árnyéka a lejtő
P(x,y)
pontjába kerül. Az elrendezés [yz]
síkban lévő vetülete a 2. ábra alsó része. Most is a Nap
A(δ,τ),
m(δ,τ)
pillanatnyi értékeitől függő x(τ),
y(τ)
koordinátákat keressük. Rendezések és egyszerüsítések után a
keresett koordináták:

Az
előzőekhez hasonlóan küszöböljük ki a közbülső A(δ,τ),
m(δ,τ)
változókat. Újabb rendezés és egyszerüsítés után a
kényelmesebb alak:

ahol

C₄
= tan(δ)×tan(φ-i)

Ezekkel
a formulákkal tetszés szerinti (φ,i)
jellemzőkkel bíró lejtőkhöz, (τ)
időpontokhoz és (δ)
évszakokhoz számíthatjuk, majd rajzolhatjuk a lejtőre merőlegesen
álló, (G)
magasságú gnomon végpontjához tartozó P(x,y)
árnyékpontok sorozatát, azaz megfelelő feliratozás mellett
kirajzolhatjuk a Nap éves illetve napi útját, egy napóra skáláit.
Ha az árnyékfelfogó sík vízszintes, azaz i
= 0, akkor a C₄
= C₂
és C₆
= C₁
egyenlőségek adódnak az előzőek szerinti lelölésekkel
összhangban.

Legyen
most az egyik egyenes a helyi délkör síkjában is, ekkor ez lesz a
délköri szál, és így egyúttal a helyi koordinátarendszer y
tengelyével is párhuzamos lesz. Legyen a másik szál e délköri
szálra merőleges, azaz kelet-nyugati irányú, s így az, az x
tengellyel lesz párhuzamos. Ezek a megkötések az asztali napóra
működésének elemzése (az árnyék-képzés mikéntje)
szempontjából nem jelentenek korlátot, de a további számításokat
egyszerüsítik.

A
skálasíkkal párhuzamos szál árnyéka önmagával párhuzamosan
mozdul el a Nap vándorlása során. A Nap pillanatnyi helyzete
(iránya, magassága) a párhuzamosságot nem befolyásolja. A
kelet-nyugati irányú keresztszál árnyékának helye (ez az
árnyékpont y
koordinátája, ha kellően hosszú a szál) a Nap magssági szögétől
függ, míg a kellően hosszú délköri szál árnyéka (az
árnyékpont x
koordinátáját) jellemzően a Nap irányszöge határozza meg.

Ha valamelyik
szálat önmagával párhuzamosan felemeljük vagy leszüllyetjük,
árnyékának napi mozgása csak annyiban változik, hogy az eredeti
és az új távolság arányának megfelelően gyorsabban/lassabban
(azaz időegység alatt nagyobb/kisebb mértékben) fog elmozdulni.
Ezért a különböző magasságban lévő szálak árnyékainak
egymáshoz viszonyított helyzete, s így az árnyékok metszéspontja
is el fog térni eredeti, a gnomon-csúcs adta árnyékponttól.
Ennek az eltérésnek az ismerete adja azt a lehetőséget, hogy az
óraskála vonalait igény szerint, kisebb-nagyobb mértékben
átalakíthassuk.

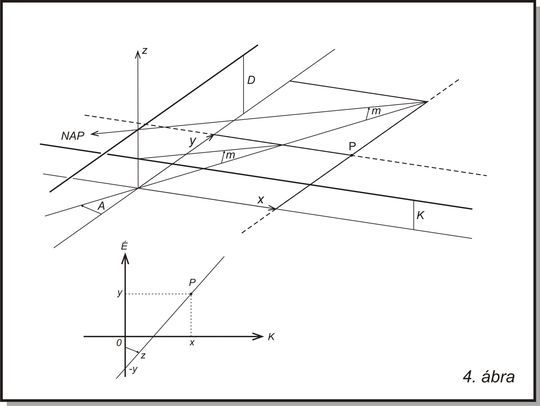Két
szál vízszintes síkkal (vázlat).

Legyen
tehát az [x,y]
skálasíktól a délköri szál D
és a kersztszál K
távolságra és a szálak legyenek párhuzamosak a koordináta
tengelyekkel (3. ábra). Ezeket a távolságokat helyettesítsük a G
gnomon csúcspontjának árnyékát megadó előzők kifejezésekbe
úgy, hogy D-vel
az x
és K-val
az y
irányú távolságokat számíthassuk. Ekkor kapjuk a P[x(
δ,τ,D);y( δ,τ,K)]
árnyékpontok koordinátáinak képleteit:

ahol ezek a
rövidítéseket is használjuk:

B
= K×tan(φ-i)

Ezek
azok a képletek, amelyekkel kényelmesen számíthatjuk a lejtőn
lévő kétszálas napóra skála pontjait és vonalait.
Természetesen a vízszintes asztal skáláját is ezek adják, ha
i=0
értékkel számolunk.

Most
számítsuk ki az aztali napóra skálaszögeit a 4. ábrán látható
vázlat alapján, ahol Z
a délvonaltól mért árnyékszög a napóra skáláján, Y
a középpont eltolás.

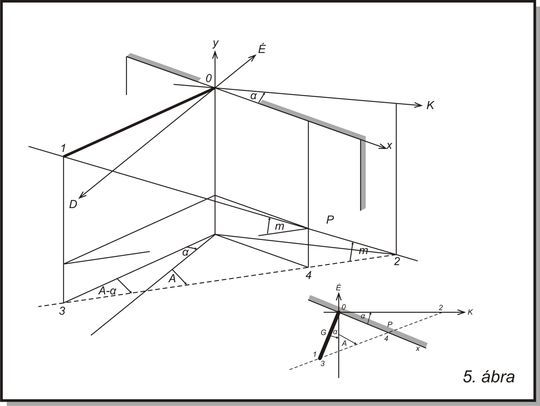Kétszálas
asztali óra skálájának számításához.

Behelyettesítés
és rendezés után kapjuk, hogy

Ha
azt akarjuk, hogy az óravonal Z szöge független legyen az
évszakoktól (azaz a C₄
és C₆
közvetítésével a Nap deklinációjától), szükséges a C₄-et
és C₆-ot
tartalmazó tagok kiejtése, tehát legyen

Ezt
visszahelyettesítve tan(Z)
kifejezésbe, kapjuk, hogy

Ha
az időszög tangensének szorzótényezője egységnyi, akkor ez az
egyenlőség azt jelenti, hogy az időszög és a skálaszög
tangense, s ezért a szögek is egymással megegyeznek: egyenlő
időközökhöz egyenlő skálaközök tartoznak. A kitűzött célt,
az egyenközű skálát tehát akkor kapjuk, ha a tetszőlegesen
megválasztott D
délköri szál távolságához a keresztszálat K=D×sin(φ-i)
távolságra választjuk. Az Y
kifejezésébe visszatéva ezt a K
értéket, a skálavonal találkozási pontjára az Y=D×cos(φ-i)
értéket kapjuk.

Ezek után az
egyszerű, kétszálas, egyenközű skálával bíró, vízszintes
asztali napórát roppant kényelmesen és gyorsan lehet elkészíteni.

• Ki kell
  jelölni az asztal észak-déli irányú délköri vonalát és
  rajta a skálavonalak tetszőleges helyen lévő pontját.

• Meg
  kell húzni e ponton átmenő és a délköri vonalra merőleges
  kelet-nyugati vonalat (ez nem az x
  tengely!), továbbá a 15°-os szögű sugárnyalábot óravonalak
  gyanánt (7,5°-al a félórákat, stb.). Az óravonalakat el kell
  látni a megfelelő számozással is.

• Kell
  még az asztal méretéhez igazodó, két egyforma, keményebb
  drótból a szögletes ácskapocshoz hasonlóra kialakított “lábas”
  árnyékvető szál. Az egyik szálat keresztszálként a
  kelet-nyugati irányú egyenes fölé, vízszintes helyzetben kell
  rögzíteni a függőleges “lábai” segítségével. Most még e
  keresztszálnak az asztallap feletti D
  magassága (!) a felülettel arányos, de érdemben tetszőleges
  lehet.

• Ezt
  követően a keresztszálnak mindkét lábát északi irányba meg
  kell dönteni úgy, hogy az asztalhoz a hely φ
  földrajzi szélességének megfelelő szögben dőljenek. Ekkor a
  vízszintes keresztszál az asztallappal továbra is párhuzamos
  marad, de lejjebb, K=D×sin(φ)
  magasságba, és Y=D×cos(φ)
  értékkel északabbra (azaz az egyébként most érdektelen x
  tengely fölé) kerül.

• Ezután
  a délköri szálat kell beállítani a “lábai” segítségével
  az asztallappal párhuzamosra, a délköri vonal fölé, szintén D
  magasságra.

Ezzel
az árnyékfelfogó sík, a két szál és az óraskála az lőzőekben
meghatározott kapcsolatba kerültek. Azaz kész az egyszerű,
pontos, kétszálas, egyenközű skálájú asztali napóránk.
Természetesen, ha az asztallap nem vízszintes, hanem i
szöggel emelkedik észak felé, a “lábakat” az asztalhoz mérten
(φ-i)
szöggel kell dönteni, azaz ekkor is a pólus felé kell
irányulniuk.

Ha
hónapvonalakat is akarunk ehhez az asztali napórához, ezek
pontjait
az alapképletekből lehet számítani, illetve e pontok alapján
rajzolhatók. A hónapvonalak egyenként az árnyékpontok
P[x(δ,τ,D);y(δ,τ,K)]
paraméteres alakjából úgy kapjuk, hogy kiküszöböljük az
időfüggést adó τ
paramétert. Végeredményeként a kúpszeletek általános
egyenletének megfelelő

Ax²
+2Bxy+Cy²+2Dx+2Ey+F=0

alakú
kifejezéshez jutunk, ahol

A=sin²(δ)/S² S=D/K

B=D=0 E=sin(φ)×cos(φ)

C=sin²(δ)-cos²(φ) F=sin²(δ)-sin²(φ)

(és
ez a D nem azonos azzal a D-vel)

A
kapott együtthatókkal ez az egyenlet az adott hely hónapvonalainak
hiperboláit fogja leírni, ha a kétszálas óra (φ,D,K)
adataival, továbbá a megfelelő hónapra érvényes (δ)
Nap-deklinációval számolunk.

A kúpszeletek
matematikájából az is ismert, hogy a hiperbola

(y–Y₀/a)²-(x–X₀/b)²=1

alakú
középponti egyenletében szereplő állandókat az előző A, B, C,
D, E, F együtthatókból a következő képletek adják:

Behelyettesítve
az adott paramétereket, kapjuk az alábbi eredményeket, ahol a
távolságok hosszúság egysége (D,K)
szerintiek:

X₀
= 0

A napóra
skálapontjait, a hónapvonalak hiperboláit és az óravonalak
egyeneseit az előzőekben leírt kifejezésekkel számíthatjuk,
rajzolhatjuk. E célra egy Excel munkalapra megfelelően beírt
függvénytáblázat és hozzá az Excel rajzolási tudománya jól
használható.

Vízszintes
gnomon árnyéka elfordult falon.

A DÉLI FAL
NAPÓRÁJA

A
függőleges, délre tájolt (Kelet-Nyugat irányú) fal óráinak
kétszálas változata (6. ábra) az azstali/lejtős változathoz
hasonlóan számítható. Egyenszögű skálával bíró változatot
a déli falra az előbbi képletekkel lehet készíteni, ha i=90°-os
dőlésszöggel számolunk.

Két
szál függőleges fallal (vázlat).

AZ
ELFORDULT FAL NAPÓRÁJA

A
kelet-nyugati irányból elfordult fal kétszálas napóráján
egyenletes lépésközű és pontos óraskálát csak akkor
kaphatunk, ha a szálaknak nemcsak a faltól való távolságát,
hanem a szálak hajlásszögét is a következő (levezetés nélkül
közölt) képletek szerint számítjuk. Ezt az elrendezést és a
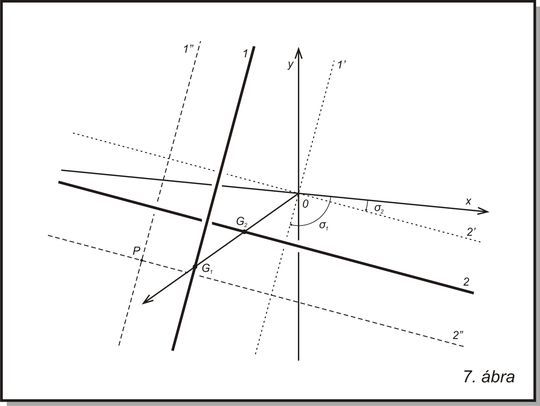
további, újabb jelöléseket a 7. ábra értelmezi, és mutatja.

{mosimage}Elfordult
függőleges fal kétszálas napórája általános helyzetű árnyékvető
szálakkal.

A
függőleges és elfordult falon a koordináta rendszer y
tengelye a fal és a délköri sík metszésvonala, az x
tengely a fal egyik vízszintes egyenese. Az [1]
jelű délköri szál
a faltól G₁
távolságra van, a [2]
jelű keresztszál
G₂-re, és
természetesen mindkettő párhuzamos a fallal. A keresztszálnak az
origón átmenő [2′]
párhuzamos árnyékvonala az x
tengellyel σ₂
szöget zár be, a délköri szál origón átmenő [1′]
árnyékvonala σ₁
szöget (+ előjelek a rajz szerint).

Az
árnyékvető szálak árnyéka [1”]
és [2”]. Ezek az
ábra szerint P(x;y)
pontban metszik egymást, melynek koordinátáit a

kifejezések
határozzák meg. Itt α
(elfordulás)
a függőleges fal normálisa és a délkör síkja közötti szög,
míg a Nap A(φ,δ,τ)
irányszögét és az
m(φ,δ,τ)
magassági szögét az előzőekben taglaltak szerint kell számítani.
A D,D_σ
K,K_σ
paramétereket a szálak (G_i,
σ_i)
adataiból a

G₀
= G₂–G₁

képletek
adják. Ha behelyettesítjük ezekbe az alapkifejezésekbe az
A(φ,δ,τ)
és m(φ,δ,τ)
korábban idézett képleteit, rendezés után azokat a formulákat
kapjuk, amelyek némileg hasonlítanak a korábban levezetettek
szerkezetéhez, és amelyekkel már jól lehet számolni az
óravonalak, és hónapvonalak pontjait:

a_x
= D×cos(α)

b_x
= D_σ×cos(φ)-D×sin(α)×sin(φ)

c_x
= D×cos(φ)×sin(α)+D_σ×sin(φ)

a_y
= K_σ×cos(α)

b_y
= K×cos(φ)-K_σ×sin(α)×sin(φ)

c_y
= K_σ×cos(φ)×sin(α)+K×sin(φ)

a
= sin(α)

b
= cos(α)×sin(φ)

c
= -cos(α)×cos(φ)

Ha
az x(τ,δ)
és
y(τ,δ) képletekből
kifejezzük a tan(δ)-t,
majd ezeket egymással egyenlővé tesszük, kiejthetjük az
árnyékpontok kifejezéséből a hónapfüggő deklinációs
tagokat, és csak az óravonalak
egyenlete marad meg. Rendezés után az óravonalak különböző
(A×x+B×y+C = 0; y = m×x+b; stb.) alakú egyenleteit kapjuk:

[K×cos(α)×cos(τ)+K×sin(α)×sin(φ)+
K_σ×cos(φ)×sin(τ)]×x–

-[D_σ×cos(α)×cos(φ)+D_σ×sin(α)×sin(φ)+D×cos(φ)×sin(τ)]×y–

Az
óravonalak közös metszéspontja (egy képzelt árnyékvető rúd
döféspontja, az asztali óránál Y=y_T)
legyen T(x;y),
ennek koordinátái:

sin(δ)
= cos(α)×cos(φ)

A
képzelt árnyékvető rúd talpvonalának h
időszögét úgy értelmezzük, hogy ott van az árnyékpont
vándorlási szögsebességének szélső értéke, s az ehhez
tartozó Z(h)
= ƒ^×.
Ezek végképletei:

A
délvonal pontjai τ
= 0
helyettesítésével az alapképletekből:

Innen
kiküszöbölve az m
magassági szöget, a délvonal és jellemzői:

A
délvonal Z(12:00)
skálaszögére:

A
délvonal és az y
tengely közötti δ
szögre:

Ha
azt akarjuk, hogy az óravonalak egyenszögűek legyenek (ennek
jelzésére szolgál a felső indexként használt ^×),
akkor az [1] jelű, eredetileg függőleges (de most már
elfordítható) délköri szál σ₁
hajlásszögéhez a [2] jelű keresztszálat σ₂^×
hajlásszögűre kell állítani:

továbbá
a G₁
száltávolsághoz ezt a másik szálat

távolságban
kell tartani a falhoz mérten.

Ha
azt akarjuk, hogy a skála óravonalai ne csak egyenszögűek
legyenek,
hanem az árnyékvető szálak merőlegesek is legyenek egymásra,
akkor az első szálat a talpvonalra merőlegesen kell a faltól G₁
távolságban elhelyezni, míg a másodiknak a talpvonal feletti G₂^×
távolságban kell lennie. Azaz:

σ₁^×
= h±90°

G₂^×
= G₁×sin(g)
= G₁×cos(α)×cos(φ)

A szálak természetesen egymással és a
fallal most is párhuzamosak.

VÁLTOZATOK A FALIÓRÁK SKÁLÁIRA

Mivel a szálakat összesen 4 méret adat
határozza meg, az alapképletekben jószerével tetszőlegesen
megválasztható 4 paraméterünk van. Az ezekkel való zsonglőrködés
további számtalan lehetőséget ad a skálák módosítására.
Néhány példa:

A
délvonal adatait az előbb úgy határoztuk meg, hogy a τ
= 0
feltételt helyettesítettük az alapegyenletekbe. Ha a Nap m(φ,δ,τ)
magassági szögét tesszük nullává, akkor azt az esetet
vizsgáljuk, amikor a Nap éppen a látóhatáron van. Ekkor két
eredményre juthatunk. Az első, mint ismeretes, hogy ekkor a Nap
kelésének (vagy nyugvásának) τ_K
időszögét kapjuk az m(φ,δ,τ)=0
egyenletből:

cos(τ_K)
= -tan(φ)×tan(δ)

A
másik eredményt (a horizont vonalat) akkor kapjuk, ha az
m(φ,δ,τ)=0
összefüggést az árnyékpont alapképleteiben vesszük figyelembe.
Azaz megkeressük a skála azon pontjait, amelyeket a kelő/nyugvó
Nap hoz létre (ha a látóhatárt eltakaró házak, fák, stb. nem
akadályozzák ebben). Ismét eltekintve a részletesebb
levezetésektől, a kétszálas napóra τ_K
időszöghöz
tartozó horizont skála vonalát [Z_K(τ_K)]
az

egyenlet írja
le. Általános esetben, az alapkifejezésekből adódik:

Ha
függőleges horizontvonalat akarunk (Z_K
= 0°), akkor innen a tetszőleges, de 0°-tól és 90°-tól
különböző hajásszögű szálakra a

feltételeket
kell teljesíteni. Vízszintes horizontvonalhoz (Z_K
= 90°) valamelyik szál legyen vízszintes (σ = 0), továbbá a G₁
≠
G₂
is teljesüljön. Ha Z_K
= 45°-os hajlásszögű horizontvonalakat akarunk, tan(Z_K)
= 1 miatt a szálak magasságára vonatkozó követelmény:

A
kétszálas asztali napórák babiloni rendszerű óraskálázásának
alapegyenleteit elsőként H.
Michnik
ismertette. Ha a napkeltétől számított B
babiloni óra óravonalának y=ƒ(x)
skálafüggvényét keressük, a

G₁×sin(φ)×cos(φ)×[1-cos(B)]×y–G₂×cos(φ)×sin(B)×x
=

=
G₁×G₂×{1-[1-cos(B)]×cos²(φ)}

képlettel
kell számolni. Ezek az óravonalak egyúttal a

G₂×cos²(φ)×x²+G₁²×sin(2φ)×y+G₂×G₁²×cos(2φ)
= 0

egyenletű
parabola burkoló érintői. Ezekre az óravonalakra is érvényes a
skála egyen-szögűségére korábban levezetett összefüggés.
Azaz, ha

akkor
az óravonalak Z(B)
szögei egyenlők a B
(babiloni rendszerű) óraszögek felével: Z
= B/2.
Az itáliai rendszer óravonalait lényegében a babilóniai
vonalaknak az É-D irányú koordináta tengelyre való tükrözésével
és átskálázásával is megkaphatjuk.