Hagyományos módszerek

A hagyományos rajzolás során a legnehezebb feladat egy pontos vázlat elkészítése: nem mindig tudjuk pontosan megtartani az alakzatok méreteit és az elhelyezkedéseit. Ha például elkezdjük lerajzolni egy bonyolultabb kráter falát, akkor mire körbeérnénk, a vázlatunkon még mindig nagyon messze vagyunk a kiindulási ponttól. Számtalan módszer terjedt el a pontosság növelésére. A legalapvetőbb mikor geometriai formákat képzelünk az alakzatokba: pl. egyenlőszárú háromszögeket, íveket. Nem túl pontos ez a módszer, hiszen kétszer is meg kell becsülnünk az arányokat. Egyszer, mikor a szemünkkel felmérjük a látottakat, másodszorra, mikor papírra vetjük őket. Bár nem ez a legpontosabb, de ez a legegyszerűbb hiszen semmilyen segédeszköz sem kell az alkalmazásához.

Egy másik bonyolultabb, de rendkívül pontos módszer a szálkeresztes okulár alkalmazása. Az üvegre karcolt és kisebb részekre felosztott háló hasznos ahhoz, hogy az egyes alakzatok egymáshoz viszonyított arányát és a látómezőn belüli távolságukat pontosan felmérjük (ilyenkor mindegy, hogy a szálrendszer beosztása mekkora valós szögértéket jelent). A merőleges vonalakat tartalmazó szálkeresztes változatnál is nagy segítséget jelent egy mérőlemezes okulár, hiszen ennél a merőlegestől eltérő szögek becslése helyett pontosan leolvashatjuk. A rajzolás ezekkel az okulárokkal is a „háromszögek módszere” szerint zajlik, azonban itt az észlelt alakzatok között jól azonosítható háromszögeket segédvonalként – a precíz vázlat készítése érdekében – célszerű felrajzolni a rajzlapra. E vonalak mentén már könnyen, gyorsan és pontosan elkészíthető az észlelt terület vázlata. A háromszögek csúcsainak olyan részleteket válasszunk, amelyek fényváltozás szempontjából rövid idő alatt stabilak, ellenkező esetben (pl. ha egy hosszú árnyék széle esetén) már a pár perces rajzolás alatt használhatatlanná válhat a segédvonalakból felvázolt szamárvezető.

Régóta alkalmazzák azt a módszert is, miszerint az észlelés előtt a kiszemelt alakzat elnagyolt körvonalait lemásolják egy térképről. Így már előre meg van az alakzatok mérete és elhelyezkedése így a távcső mellett már csak az apró részletek pontos berajzolásával kell törődni. Ennek a módszernek a legnagyobb hátránya, hogy a libráció miatt a valóság el fog térni a vázlatunktól. Ha nagyon nagy az eltérés, az rendkívül megnehezítheti az előre elkészített skicc használatát.

Digitális technika

Nemrégiben jutott el hozzánk Méhes Ottón fordítása révén egy új módszer, melyet Peter Grego dolgozott ki. Az eljárás az előző módszer kibővítése a digitális képrögzítés felhasználásával. Míg az előző módszerben egy térképet használunk fel a körvonalak lerajzolásához, addig ennél egy digitális felvétel alapján vesszük fel a körvonalakat.

Az észlelés kezdetekor egy felvételt kell készíteni a kiszemelt alakzatról és a környékéről. Mivel csak a körvonalakra van szükségünk, ezért egy gyengébb minőségű felvétel is elég: ha ügyesen csináljuk akkor egy egyszerű kompakt digitális géppel és odatartásos módszerrel is megfelelő minőségű képet készíthetünk. Egy területről több felvételt is készítsünk, hogy a légkör hullámzása és a képkészítési módszerünk hibái miatt.

Miután kiválasztottuk a legjobban sikerült felvételt, azt számítógéppel feljavíthatjuk, beforgathatjuk és méretre vághatjuk. Ha késszen vagyunk a rajzzal, nyomtassuk ki, és kezdődhet a körvonalak átrajzolása. A vázlat elkészítésére szánt lapot tegyük a kinyomtatott kép fölé, és másoljuk át az alakzat és a környező objektumok körvonalait. A másoláshoz ablaküveget vagy alulról megvilágított üvegtáblát is használhatunk. Mivel általában a felvételeken nem lehet tisztán kivenni a körvonalakat, ezért csak a nagy befoglaló formákat rajzoljuk át halványan, hogy később könnyen javíthassunk rajtuk.

A távcső mellett a körvonalakat használva „szamárvezetőként” rajzoljuk be a legapróbb alakzatokat is. Mivel az alapvető arányokat már berajzoltuk a felvétel alapján, ezért sokkal könnyebb a vázat elkészítése.

Legelőször a terminátor közvetlen közelében lévő Julius Caesar- krátert rajzoltuk le ezzel a módszerrel. A sok apró részlet miatt kb. 40 percig tartott, mire lerajzoltuk a kráter peremét és meglepődve tapasztaltuk, hogy miután körbeértünk, a vázlaton is minden ott volt, ahol a látómezőben, és eközben csak a részletek berajzolásával kellett törődni.

Felmerülhet a kérdés, hogy nem „csalás”-e ez a módszer, hiszen nem csak vizuális módszert használunk a rajzunk elkészítéséhez. Ugyanakkor figyelembe kell vennünk, hogy nem feltétlenül csak az a célunk, hogy lerajzoljuk a Holdat, hanem hogy a lehető legpontosabban megörökítsük a látottakat. A rajzolásnak és a felvétel készítésnek is meg vannak a maga előnyei és hátrányai. Ha a fenti módon kombináljuk a két észlelési módszert, akkor egy, a két módszerrel külön-külön elérhető eredménynél sokkal jobbat kaphatnk-

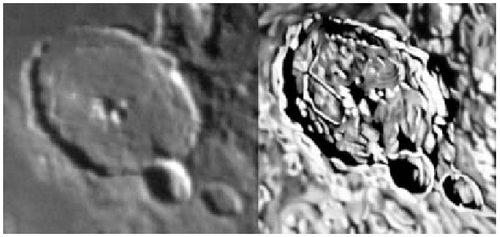
Példaként álljon itt Peter Grego csodálatos rajza a Gassendi-kráterről bizonyítva, hogy egy nem túl jól sikerült felvételből is lehet egy nagyon jó rajzot készíteni

{mosimage}

Jakabfi Tamás